Three (Rs) Tips for Better Statistical Analysis
1. Formalise your design
A Simple Experiment
I am worried that I have a pair of loaded dice: biased to roll one number more often than expected by chance alone.
My experiment
I roll my two dice and the “biased” number shows on one die; check if both dice show the same number.
If both dice show the same number more often than chance alone would suggest, I will accept my dice are loaded.
Let’s set a P-value threshold for accepting the null hypothesis
\(H_0\): both dice are fair and show that same number by chance alone.
Live demonstration
Ooh! Risky!

Figure 1: How to bias dice by heating them in an oven at about 121degC for 10min. Don’t use a microwave or blame me for the consequences/if you get caught.
Your predictions, please
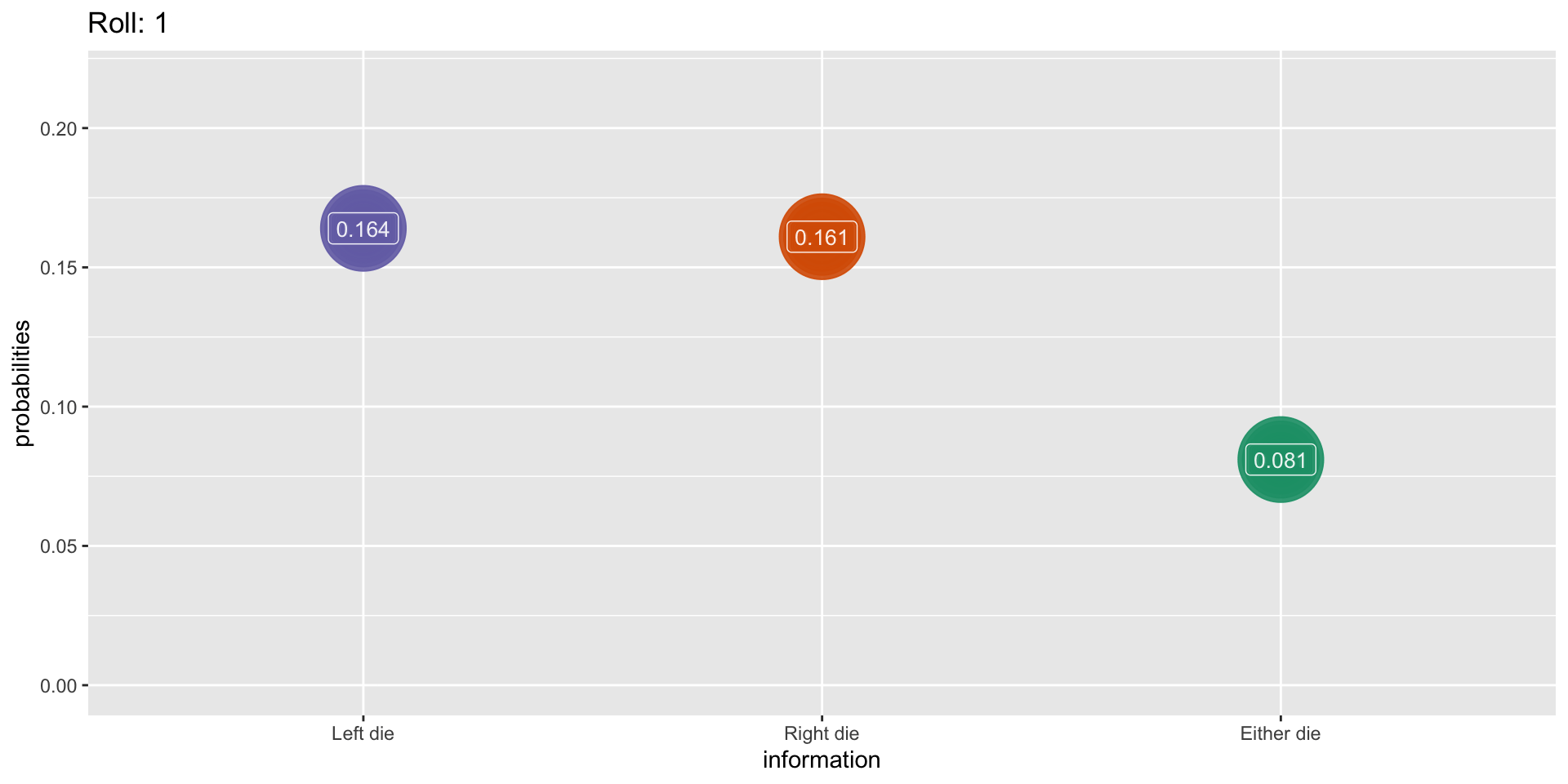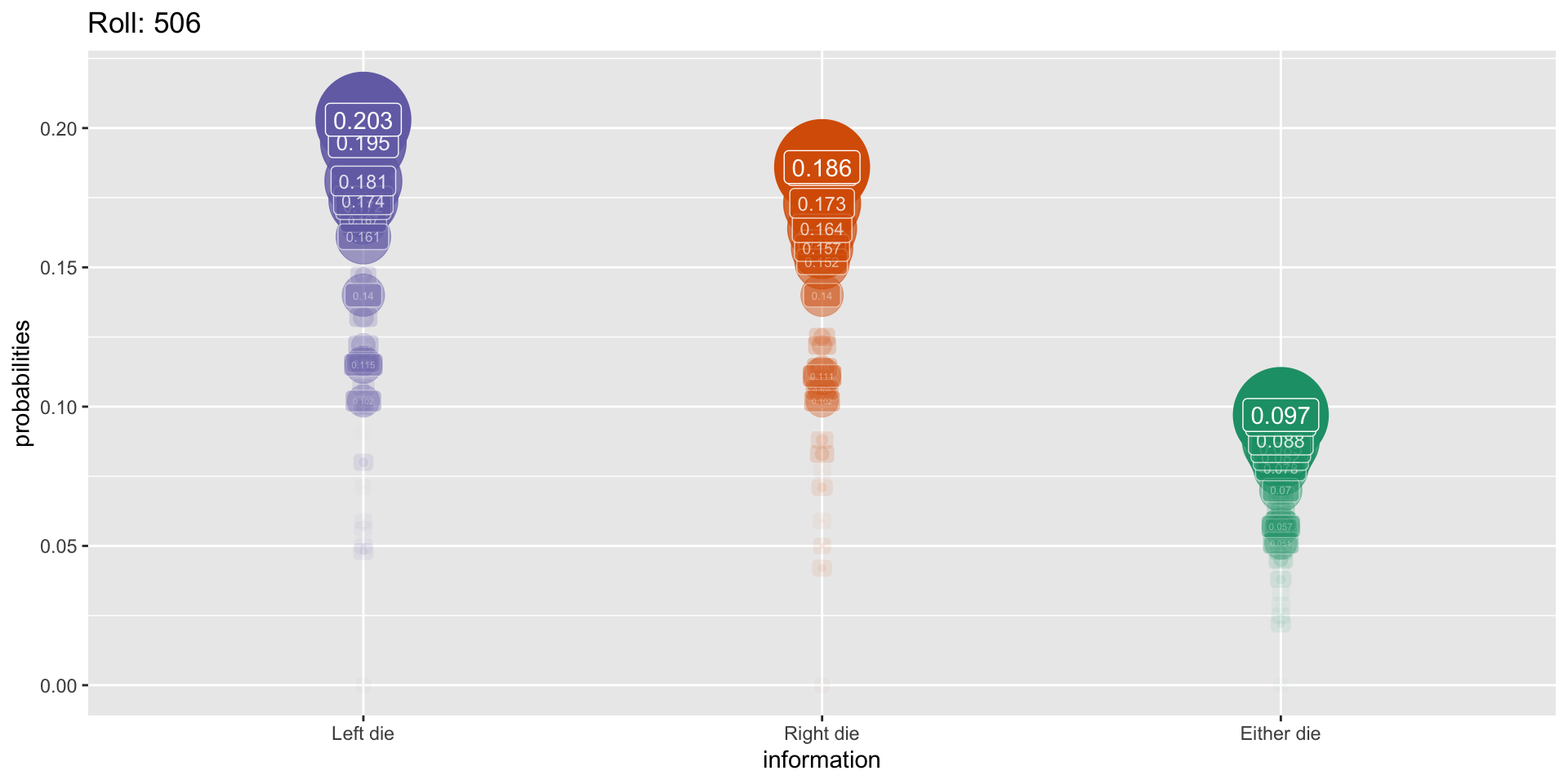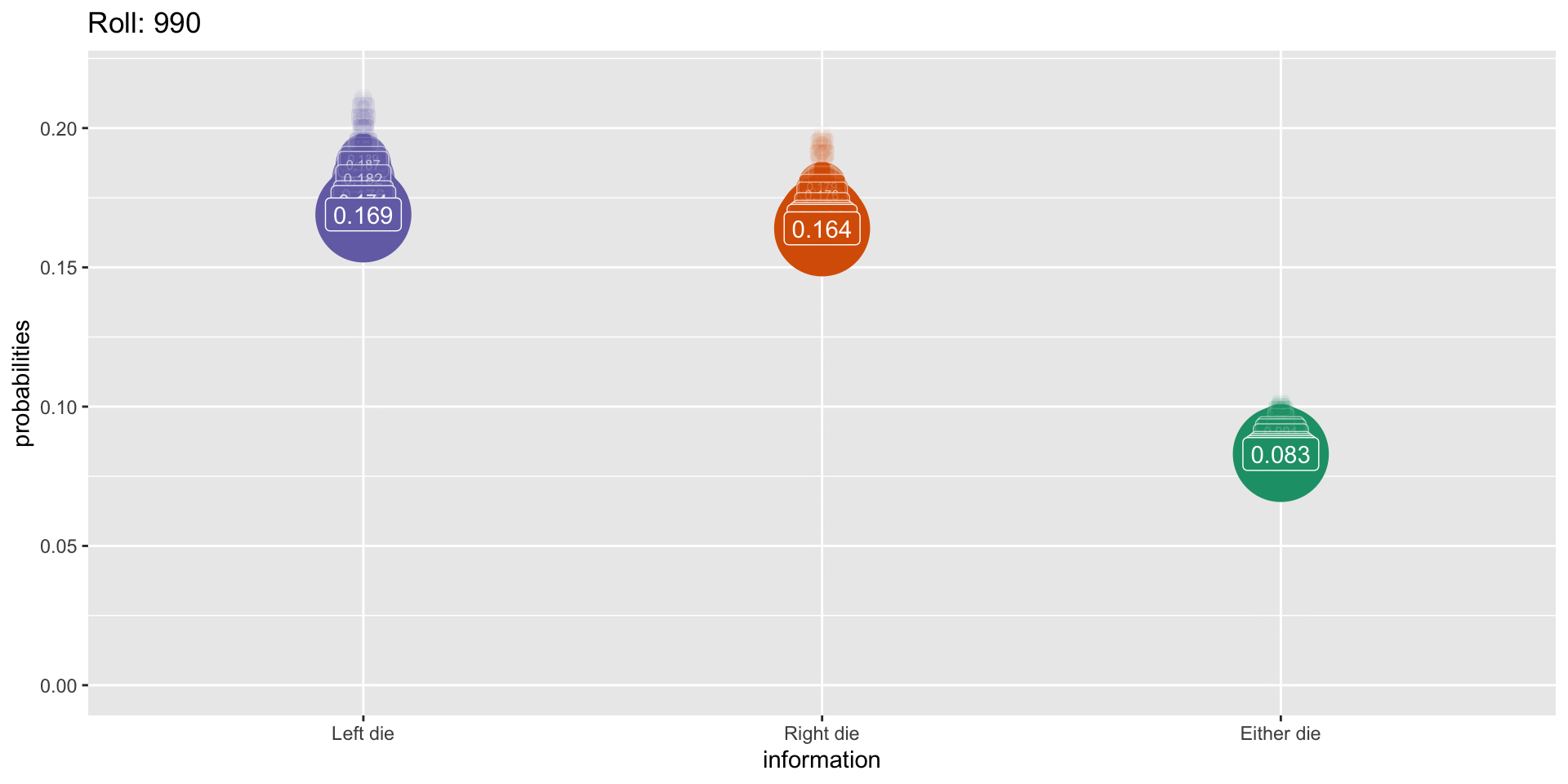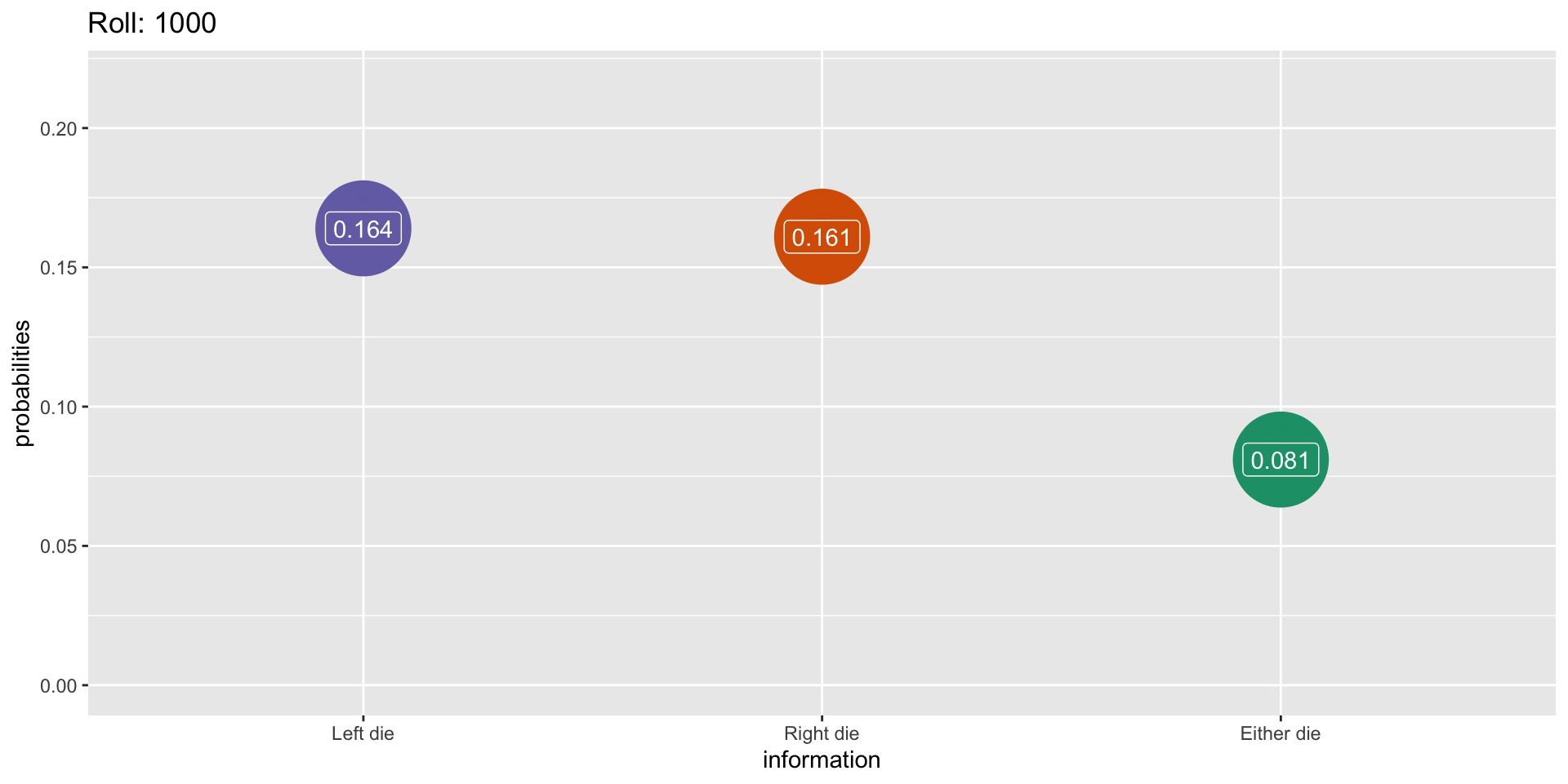
If one die shows the pre-named “bias” number, what is the probability that both dice are fair and showed the same number, by chance alone?
Probability
A definition
The probability of an event occurring is: the proportion of all possible outcomes that are that event.
Tossing a coin
Outcomes: heads or tails (two outcomes, assuming a fair coin and toss)
Probability of showing heads: \(\frac{1}{2} = 0.5\) as it is one of two outcomes
Outcomes when rolling two dice
Simulation: 1000 rolls
What This Means For Us
Caution
Verbal and written experiment descriptions can influence or disguise expected effect sizes, statistical analysis and outcomes
Talk to a statistician (or other colleague)
- what’s ambiguous to them?
- if they explain the experiment back to you, what sounds different to you?
What This Means
Caution
Verbal and written experiment descriptions influence statistical analysis and outcomes
Experimenter understanding can influence use of language
- We assume through explanatory gaps when we think we understand something.
- Clarity and precision are essential when explaining to others
- Use the NC3Rs EDA to formalise unambiguous experimental designs
Use NC3Rs EDA
Please share the EDA diagram/session with your statistician.
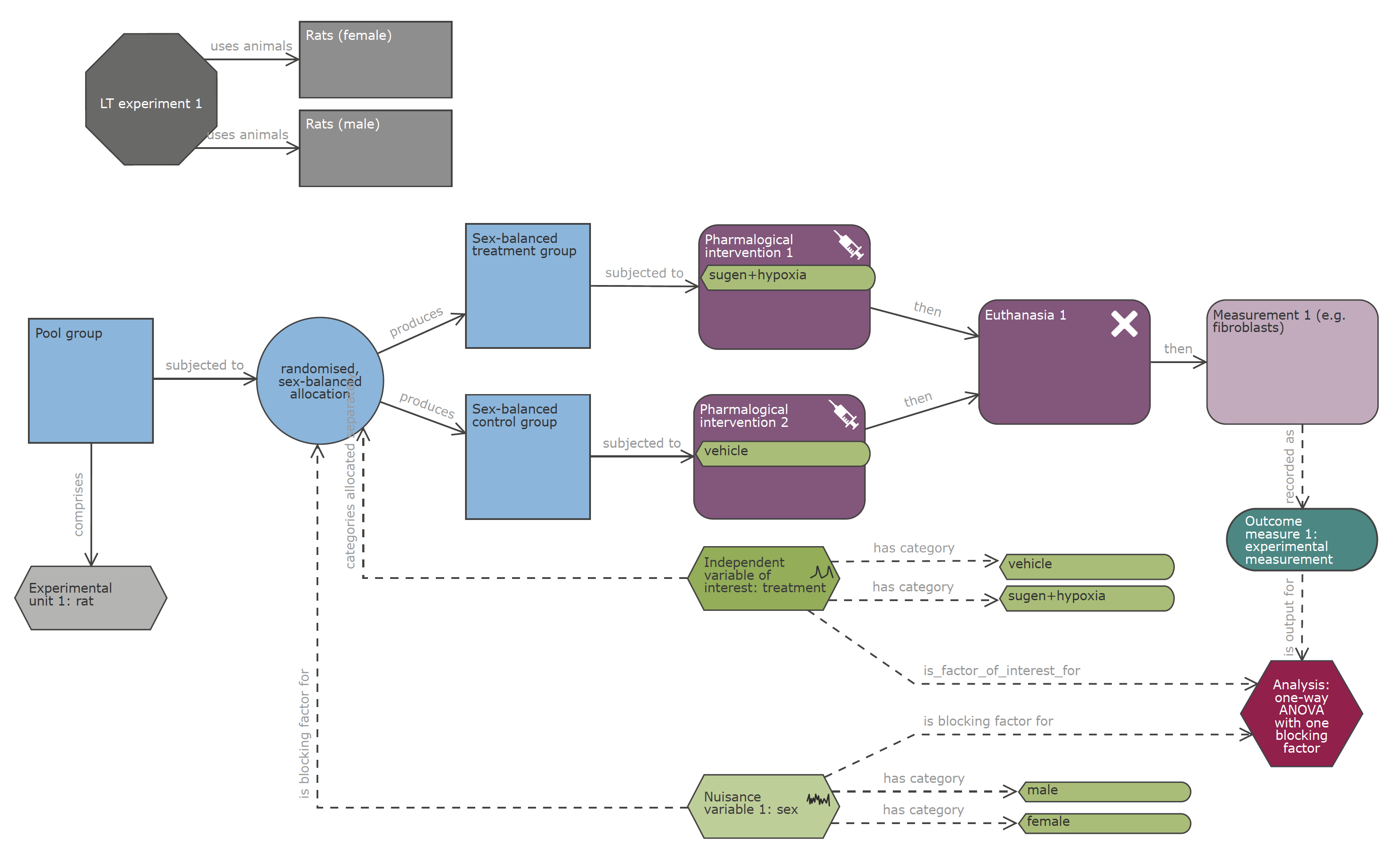
Figure 2: NC3Rs EDA forces clarification of concepts and is a focus for discussion.
2. Use ANOVA
An experimental dataset
- A control (
ctrl) and two treatments (trt1,trt2)
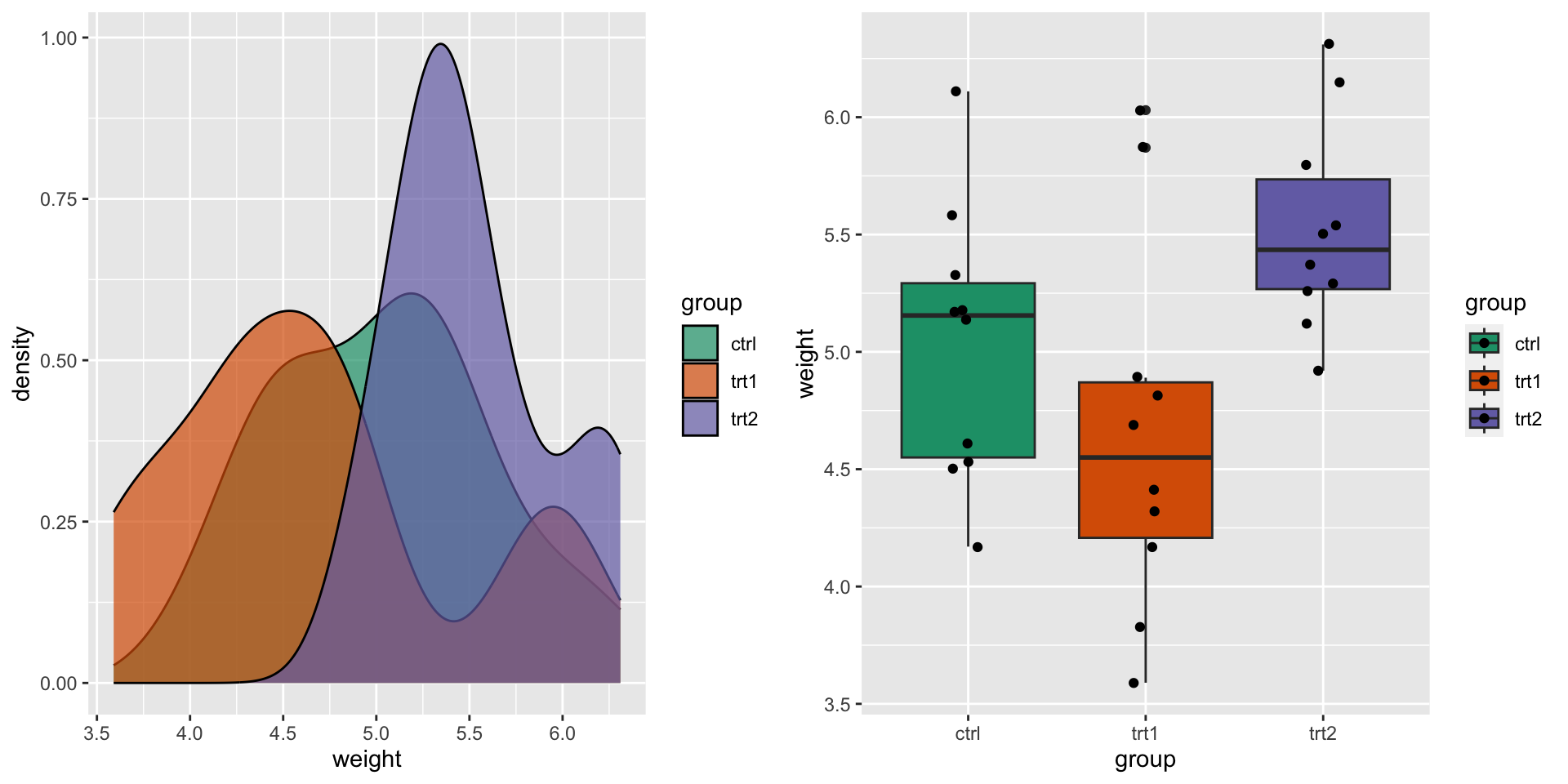
- Does it look like there are differences between the groups?
t-tests
t-tests assume that datasets are Normal distributions 1
The only input the test gets:
- mean \(\mu\), standard deviation \(\sigma\) for each group
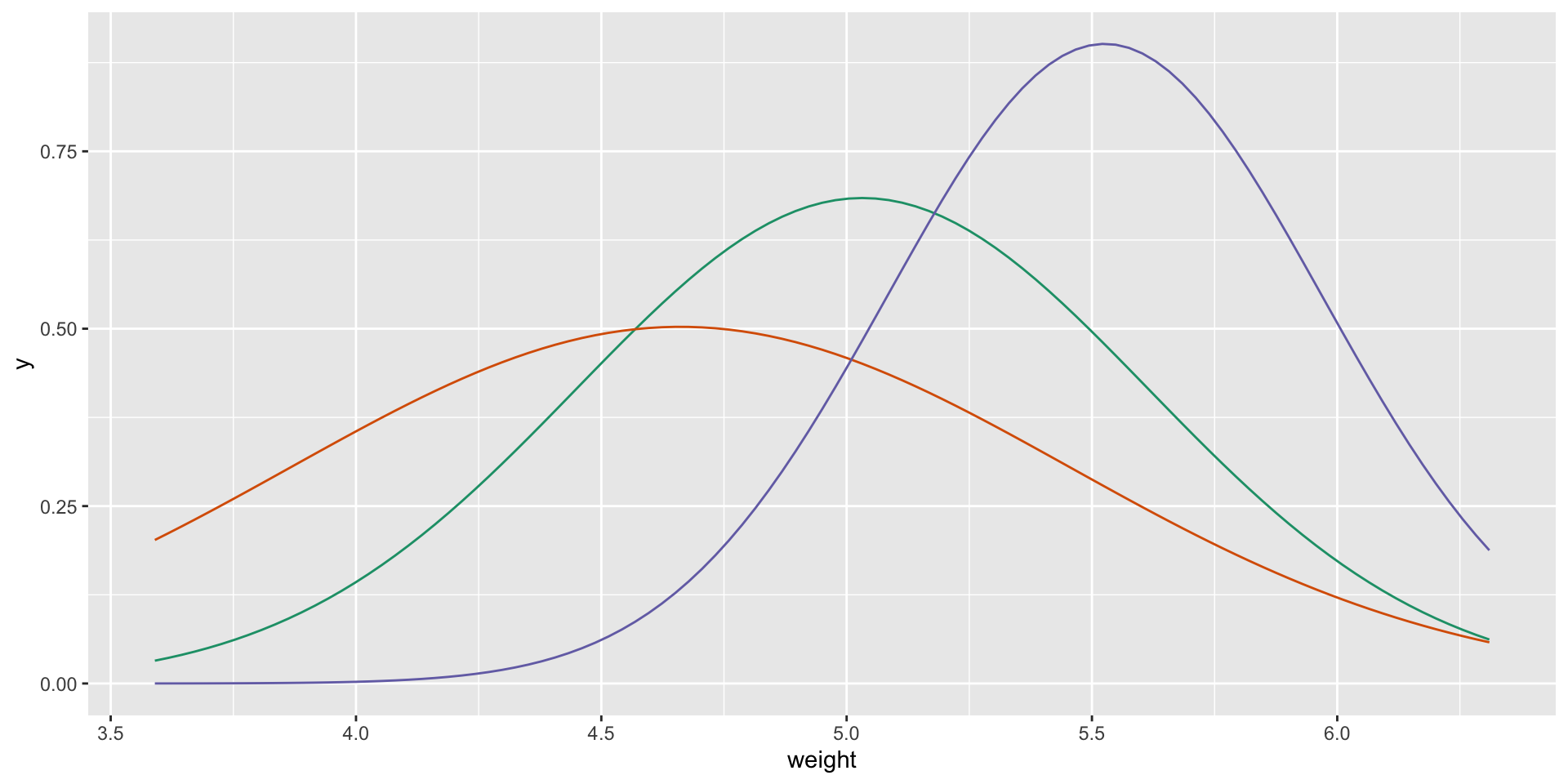
t-tests
t-tests assume that datasets are Normal distributions
The only input the test gets:
- mean \(\mu\), standard deviation \(\sigma\) for each group
| group | mean | sd |
|---|---|---|
| ctrl | 5.032 | 0.5830914 |
| trt1 | 4.661 | 0.7936757 |
| trt2 | 5.526 | 0.4425733 |
t-test results
Tip
I’d recommend R for reproducible analyses. 1
| estimate | conf.low | conf.high | p.value | |
|---|---|---|---|---|
| ctrl.vs.trt1 | 0.371 | -0.2875162 | 1.0295162 | 0.2503825 |
| ctrl.vs.trt2 | -0.494 | -0.9828721 | -0.0051279 | 0.0478993 |
| trt1.vs.trt2 | -0.865 | -1.4809144 | -0.2490856 | 0.0092984 |
Multiple tests
These p.values are not correct
For three groups, there are three pairwise comparisons.
But t-tests calculate probability for a single pairwise comparison!
Multiple t-tests on your data increase Type I error rate (at P<0.05)
- One test: P(type I error) = 0.05
- Two tests: P(type I error) = 0.0975
- Three tests: P(type I error) = 0.1427
Multiple tests
These p.values are not correct
For three groups, there are three pairwise comparisons.
But t-tests calculate probability for a single pairwise comparison!
One solution: multiple test correction
Bonferroni, Benjamini-Hochberg, etc.
- Bonferroni: divide your P-value significance threshold by number of comparisons, \(n\)
- P threshold for one comparison: \(0.05\)
- Adjusted for three comparisons: \(0.05 / 3 \approx 0.016\)
Corrected t-test results
We adjust our threshold for significance.
Which comparisons are significant at \(P=0.05\) for a single comparison, when Bonferroni corrected for three comparisons? (i.e. \(P=0.016\))
| estimate | conf.low | conf.high | p.value | |
|---|---|---|---|---|
| ctrl.vs.trt1 | 0.371 | -0.2875162 | 1.0295162 | 0.2503825 |
| ctrl.vs.trt2 | -0.494 | -0.9828721 | -0.0051279 | 0.0478993 |
| trt1.vs.trt2 | -0.865 | -1.4809144 | -0.2490856 | 0.0092984 |
ANOVA
Especially if you have data in three or more groups, use ANOVA
- ANOVA performs all comparisons for all groups simultaneously
- ANOVA does not require multiple test correction
- ANOVA can give more information than a t-test
- t-tests are a special case of ANOVA (you get the same answer either way)
ANOVA in R:
No more difficult than applying a t-test
| estimate | conf.low | conf.high | p.value |
|---|---|---|---|
| -0.865 | -1.48091 | -0.24909 | 0.0093 |
| Characteristic | p-value |
|---|---|
| group | 0.008 |
t-tests and ANOVA are related
Student’s t-test assumes equal variances
| estimate | conf.low | conf.high | p.value |
|---|---|---|---|
| -0.865 | -1.469 | -0.261 | 0.008 |
ANOVA on two groups is a pairwise Student’s t-test
| Characteristic | p-value |
|---|---|
| group | 0.008 |
t-tests and ANOVA are related
| estimate | conf.low | conf.high | p.value |
|---|---|---|---|
| -0.865 | -1.48091 | -0.24909 | 0.0093 |
ANOVA with unequal variance is a pairwise Welch’s t-test
| p.value | method |
|---|---|
| 0.0093 | One-way analysis of means (not assuming equal variances) |
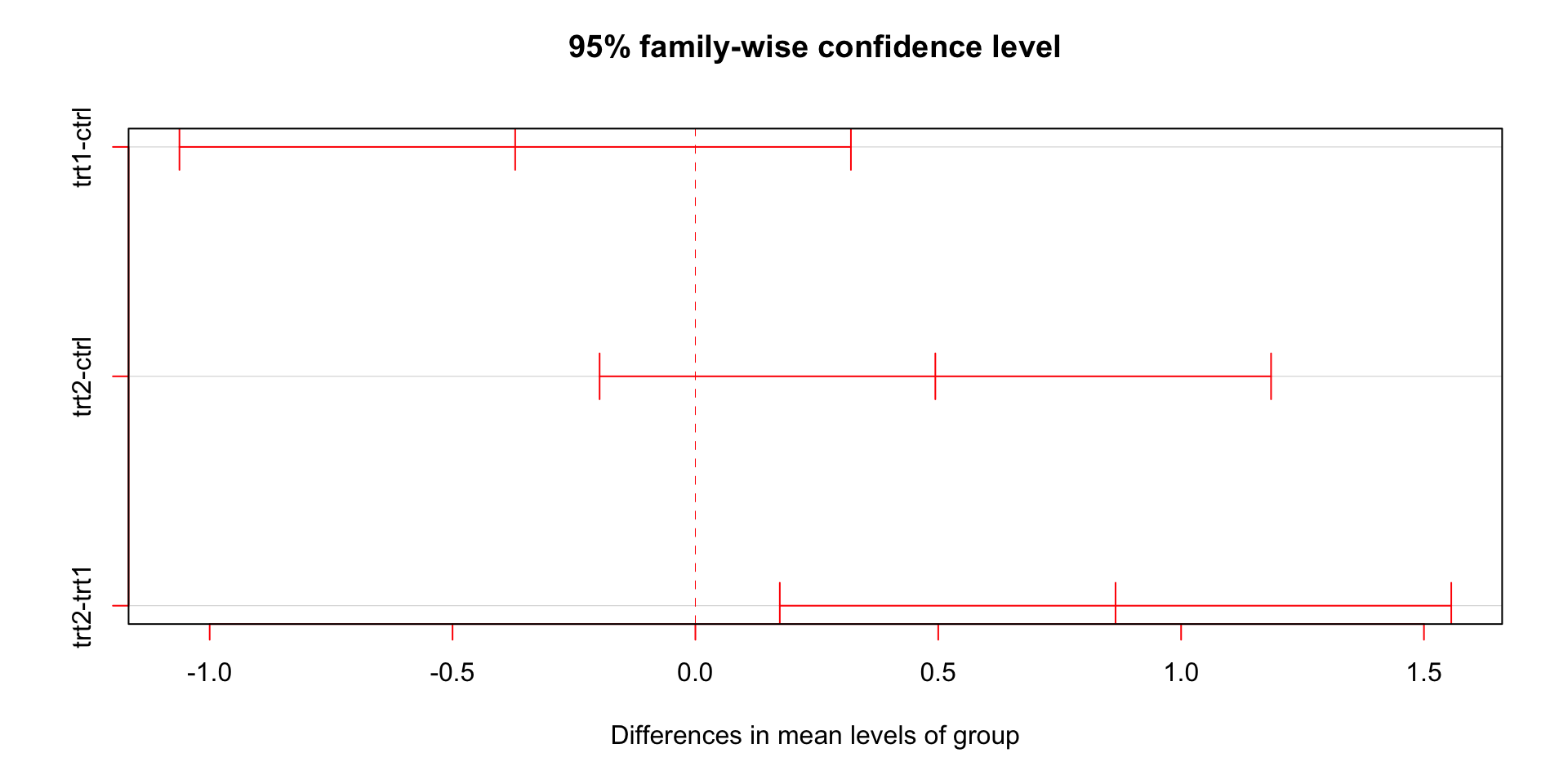
Comparing multiple groups
All pairwise comparisons with ANOVA
Use Tukey’s HSD (Honest Significant Difference)
- a common, but not the only, post-hoc test
| group1 | group2 | estimate | conf.low | conf.high | p.adj |
|---|---|---|---|---|---|
| ctrl | trt1 | -0.371 | -1.062 | 0.320 | 0.391 |
| ctrl | trt2 | 0.494 | -0.197 | 1.185 | 0.198 |
| trt1 | trt2 | 0.865 | 0.174 | 1.556 | 0.012 |
Comparing multiple groups
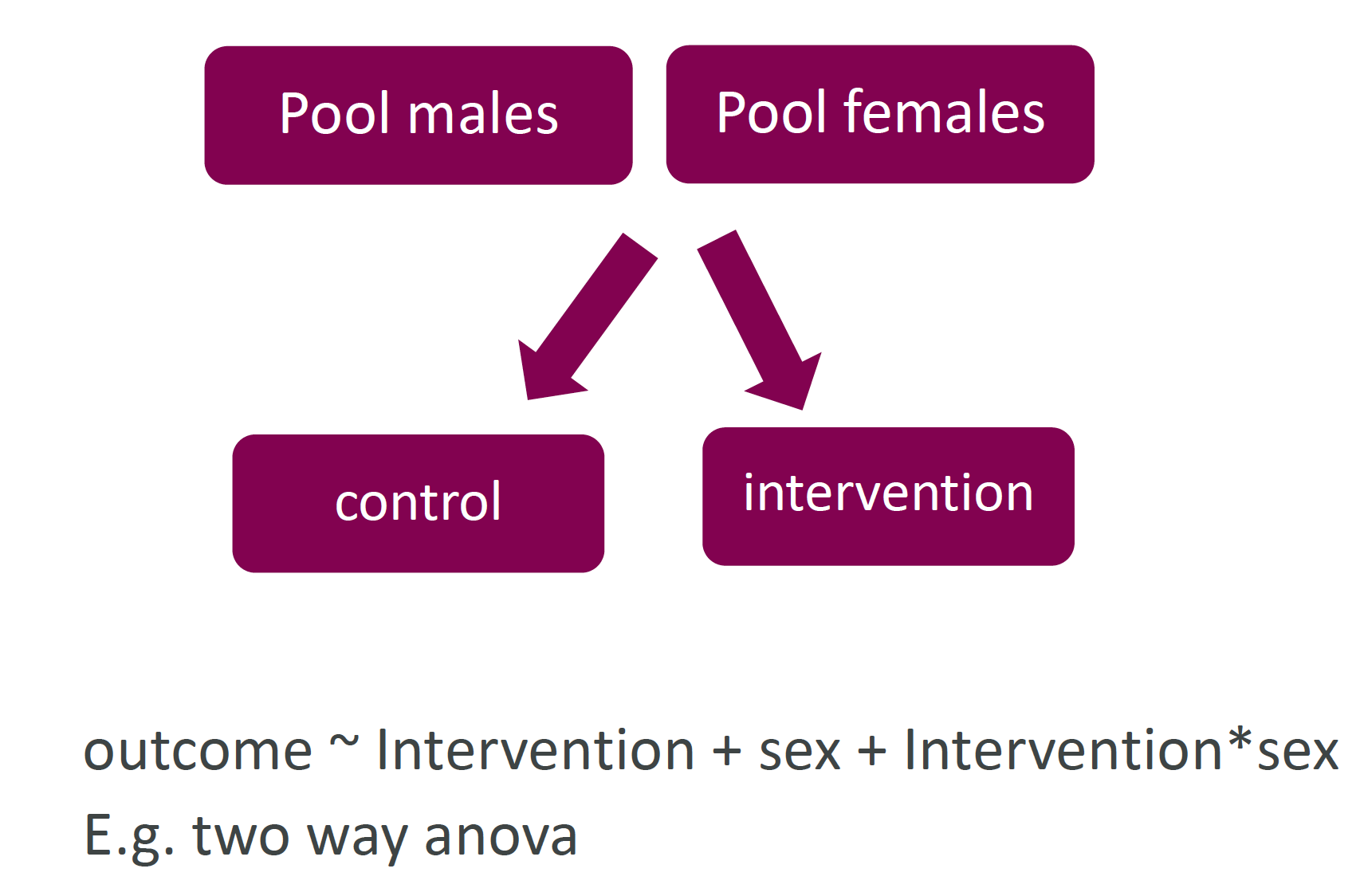
ANOVA allows blocking
This is important when using both sexes
But also if there are other batch effects to account for

Figure 3: MRC require that both sexes are used in experiments, unless there is strong justification not to.
ANOVA supports blocking

An example
Let’s look at penguins!
- Does body mass vary by species?
- (but let’s be mindful that there might be a sex difference)
| species | sex | body_mass_g |
|---|---|---|
| Adelie | male | 3750 |
| Adelie | female | 3800 |
| Adelie | female | 3250 |
| Adelie | female | 3450 |
| Adelie | male | 3650 |
| Adelie | female | 3625 |
Visualise the dataset
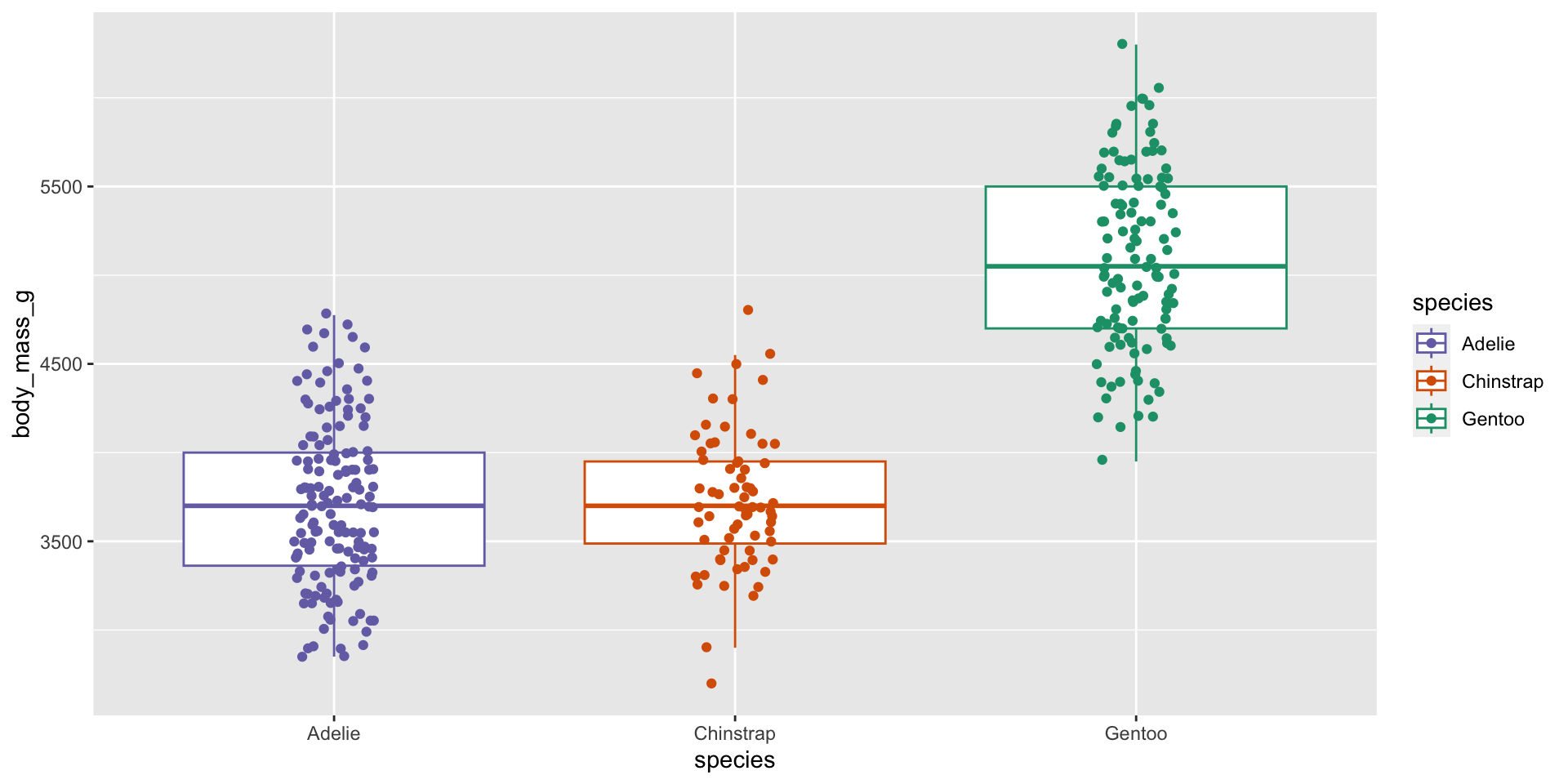
One-way ANOVA (ignore sex)
| Characteristic | p-value |
|---|---|
| species | <0.001 |
| group1 | group2 | estimate | conf.low | conf.high | p.adj |
|---|---|---|---|---|---|
| Adelie | Chinstrap | 26.924 | -132.353 | 186.201 | 0.916 |
| Adelie | Gentoo | 1386.273 | 1252.290 | 1520.255 | 0.000 |
| Chinstrap | Gentoo | 1359.349 | 1194.430 | 1524.267 | 0.000 |
Visualise the dataset (sex differences)
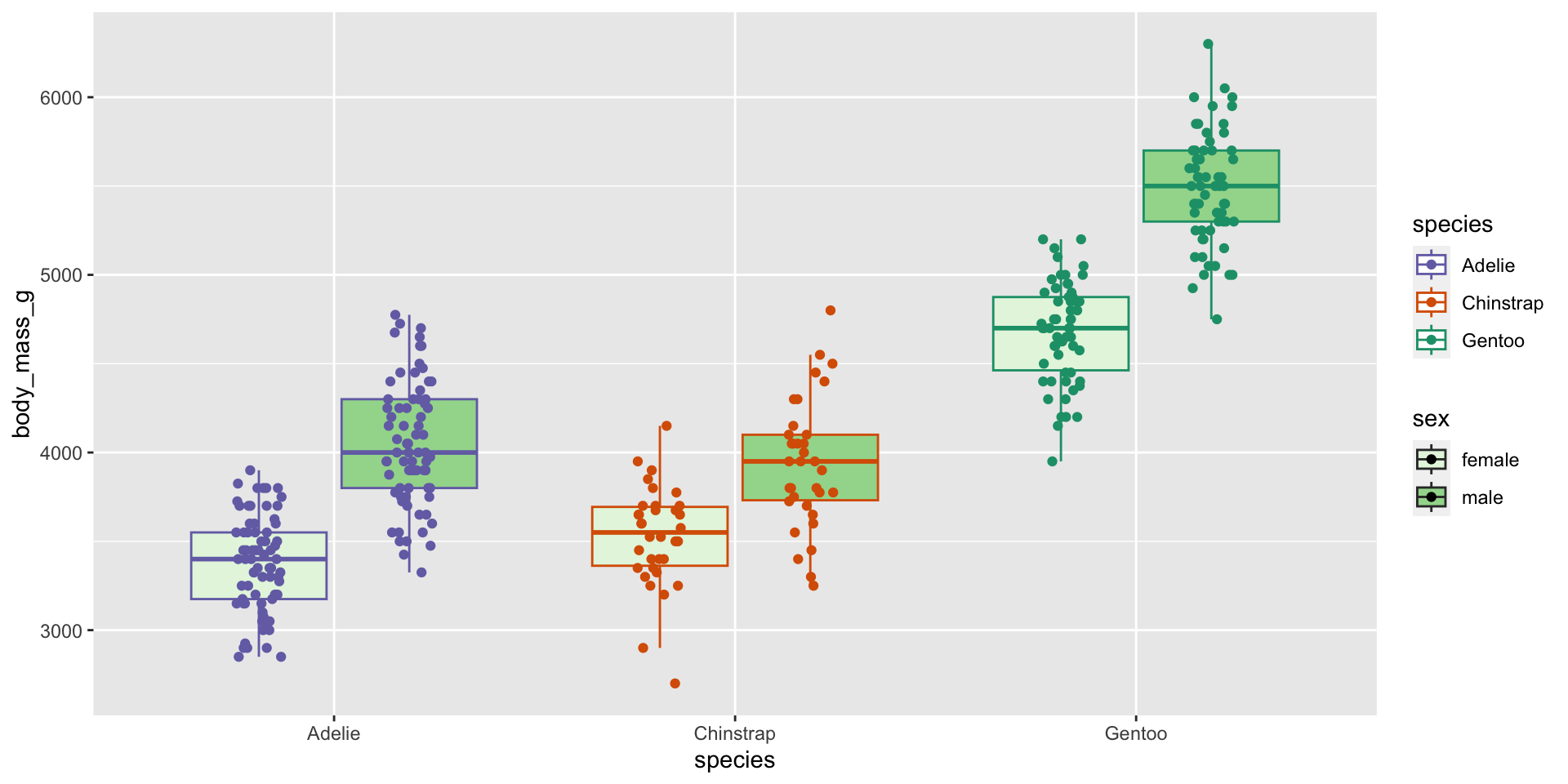
Two-way ANOVA (monitor sex effect)
| Characteristic | p-value |
|---|---|
| species | <0.001 |
| sex | <0.001 |
| group1 | group2 | estimate | conf.low | conf.high | p.adj |
|---|---|---|---|---|---|
| Adelie | Chinstrap | 26.924 | -82.515 | 136.363 | 0.831 |
| Adelie | Gentoo | 1386.273 | 1294.213 | 1478.332 | 0.000 |
| Chinstrap | Gentoo | 1359.349 | 1246.033 | 1472.664 | 0.000 |
| female | male | 667.458 | 599.193 | 735.722 | 0.000 |
Interactions between categories
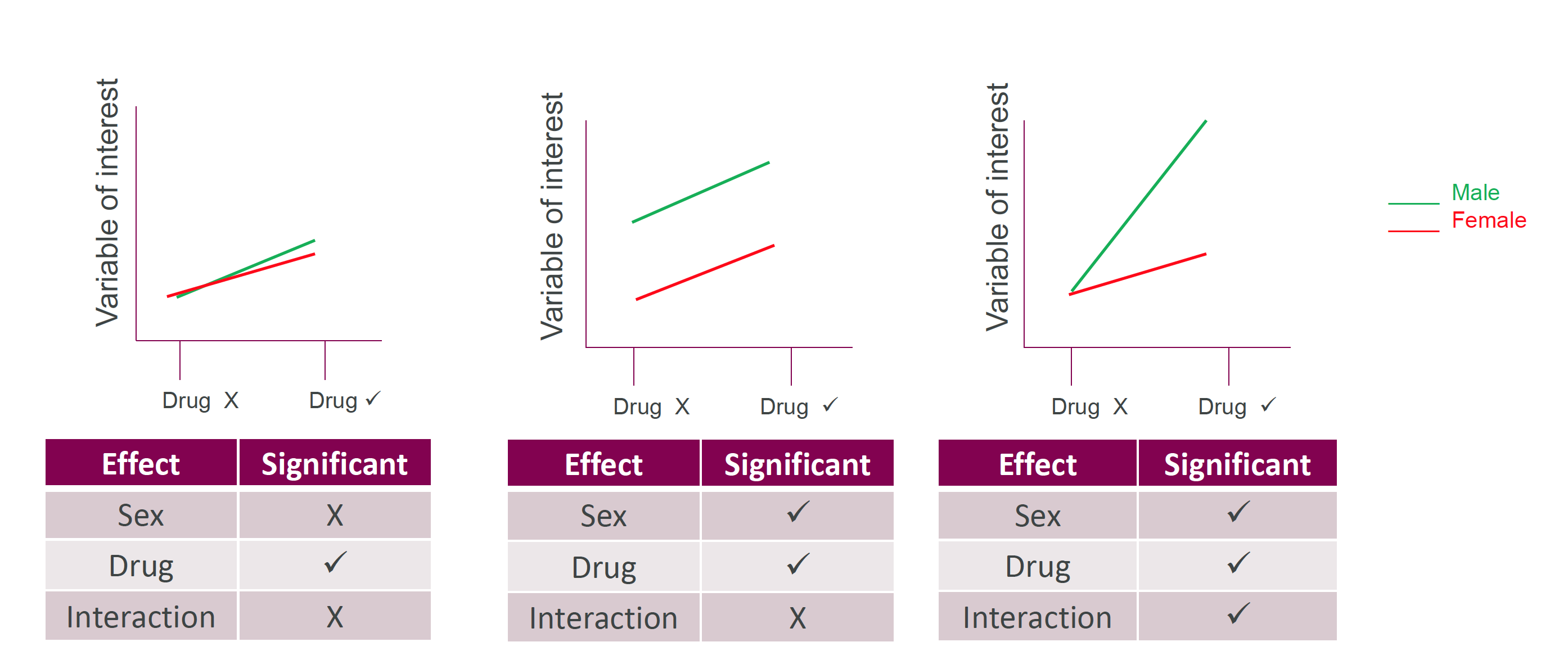
Figure 6: Two-way ANOVA lets us see interactions between categories
Interactions between categories
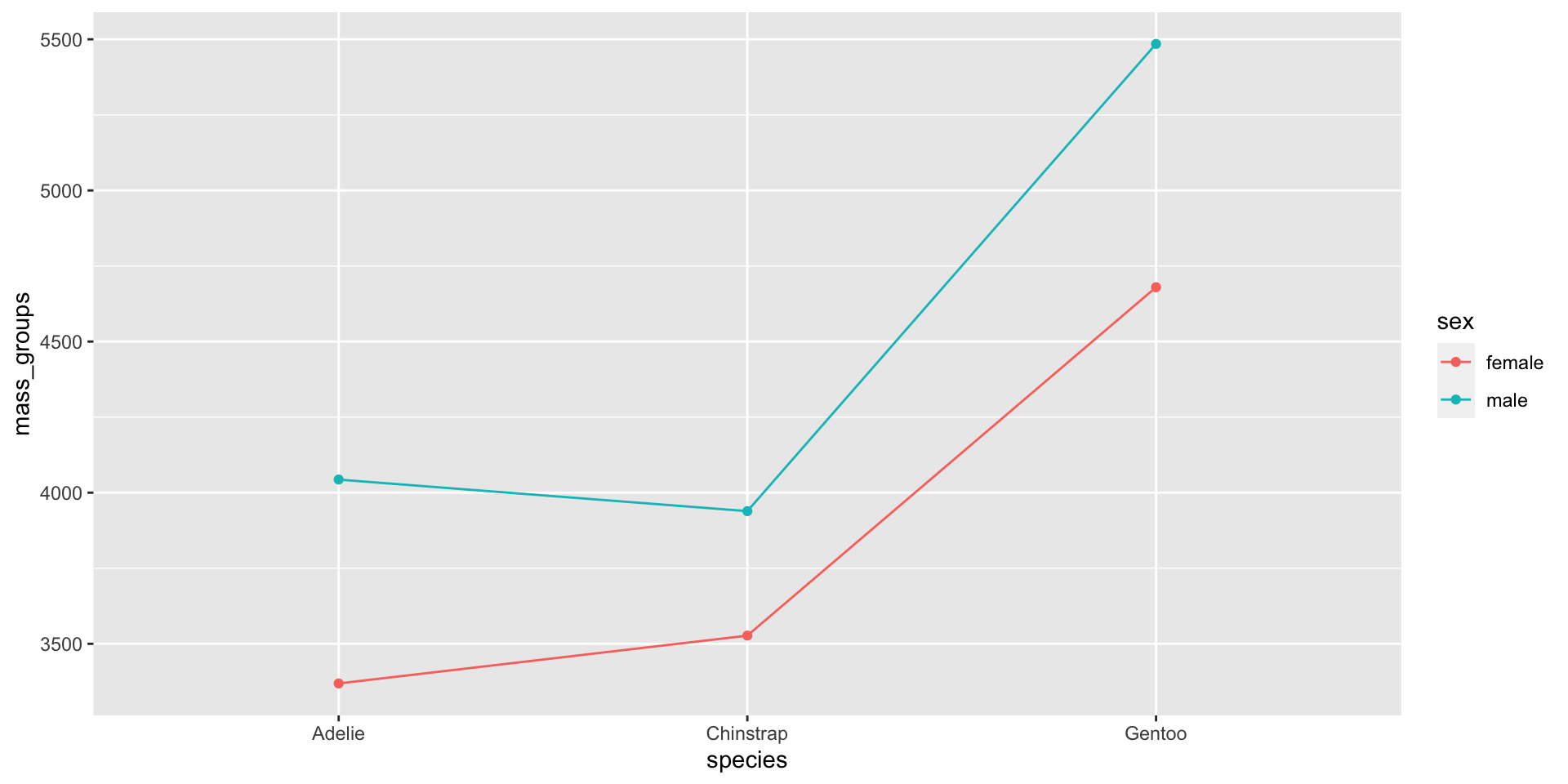
Interactions between categories
| Characteristic | p-value |
|---|---|
| species | <0.001 |
| sex | <0.001 |
| species * sex | <0.001 |
There are significant effects due to species and sex
And also an interaction between species and sex
(i.e. the influence of sex varies from species to species)
ANOVA is a regression model
Can use R’s regression tools to extract more information
| Characteristic | Beta | 95% CI1 | p-value |
|---|---|---|---|
| species | |||
| Adelie | — | — | |
| Chinstrap | 158 | 32, 285 | 0.014 |
| Gentoo | 1,311 | 1,204, 1,418 | <0.001 |
| sex | |||
| female | — | — | |
| male | 675 | 574, 775 | <0.001 |
| species * sex | |||
| Chinstrap * male | -263 | -442, -84 | 0.004 |
| Gentoo * male | 130 | -20, 281 | 0.089 |
| 1 CI = Confidence Interval | |||
ANOVA is a regression model
Using interactions and regression can be more informative
| group1 | group2 | estimate | conf.low | conf.high | p.adj |
|---|---|---|---|---|---|
| Adelie | Chinstrap | 26.924 | -82.515 | 136.363 | 0.831 |
| Adelie | Gentoo | 1386.273 | 1294.213 | 1478.332 | 0.000 |
| Chinstrap | Gentoo | 1359.349 | 1246.033 | 1472.664 | 0.000 |
| female | male | 667.458 | 599.193 | 735.722 | 0.000 |
| Characteristic | Beta | 95% CI1 | p-value |
|---|---|---|---|
| species | |||
| Adelie | — | — | |
| Chinstrap | 158 | 32, 285 | 0.014 |
| Gentoo | 1,311 | 1,204, 1,418 | <0.001 |
| sex | |||
| female | — | — | |
| male | 675 | 574, 775 | <0.001 |
| species * sex | |||
| Chinstrap * male | -263 | -442, -84 | 0.004 |
| Gentoo * male | 130 | -20, 281 | 0.089 |
| 1 CI = Confidence Interval | |||
EDA may recommend ANOVA
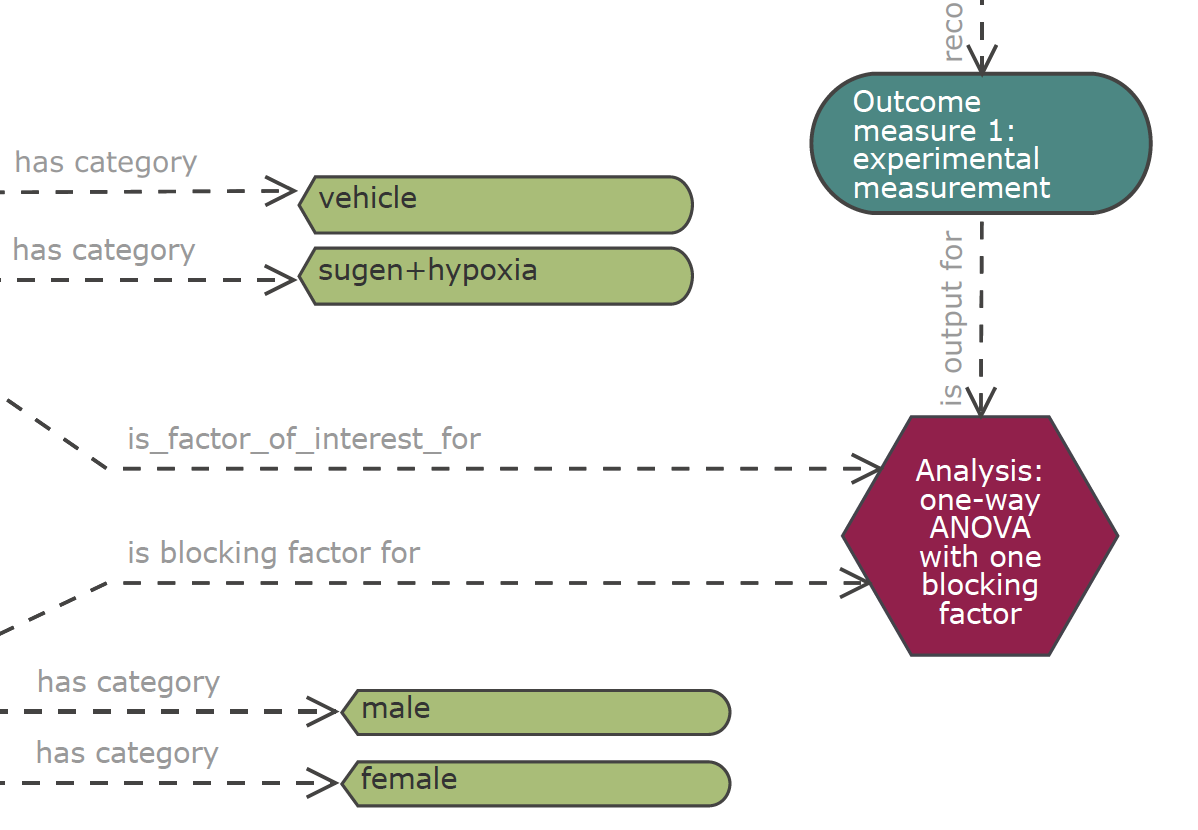
Figure 7: EDA may well recommend ANOVA
But NC3Rs EDA power calculations only cover pairwise t-tests!
3. ANOVA power calculation
EDA power calculations
NC3Rs EDA power calculations only cover pairwise t-tests
But other tools are available
RG*PowerSPSSStata- run your own simulations
G*Power
- Free software
- HHU Düsseldorf
- Windows and macOS
- Detailed manual
Supports ANOVA power calculation
G*Power on macOSPower
Statistical Power
Type II Error, \(\beta\): the probability of a false negative (missing a true positive result)
Power, \(1 - \beta\): the probability that you won’t miss a true positive result (assuming that there is one)
Statistical Threshold
Type I Error, \(\alpha\): the probability of a false positive (calling a positive result when the true result is negative)
This is the P-value threshold you set for your hypothesis tests
Calculating minimal sample sizes
For 3Rs we want to minimise individuals used
You need to know 1
- What size of effect you aim to detect
- How many groups (categories) and their layout (e.g. two species, two sexes = \(2 \times 2\))
- This allows us to calculate degrees of freedom (d.f.)
- The statistical threshold \(\alpha\) for the probability of false positives you’re willing to accept
- The statistical power \(1 - \beta\) for the probability of false negatives you’re willing to accept
Effect size in ANOVA
Effect size definition
Effect size is an interpretable number that quantifies the difference between the data and a hypothesis.
Multiple measures for this
- Cohen’s D, Cohen’s W, Cohen’s F, Pearson’s R, \(\eta^2\) (partial) eta squared, Cramér’s V, etc.
G*Power uses Cohen’s F for ANOVA
- small effect size \(f\) = 0.10
- medium effect size \(f\) = 0.25
- large effect size \(f\) = 0.40
An example
Our experiment
- Measure treatment vs control (two groups), and difference between sexes (two groups); design is \(2 \times 2\) factorial
- Numerator degrees of freedom: \((2 - 1) \times (2 - 1) = 1\)
- Number of groups: \(4\)
- By convention, we use \(\alpha = 0.05\), \(1 - \beta = 0.8\).
A priori power calculation (ANOVA): main effects and interactions
F-testANOVA, Fixed effects, special, main effects and interactions
An example
- Test family:
F tests - Type of power analysis:
A priori: Compute required sample size - given\(\alpha\), power, and effect size - Effect size \(f\):
0.4 - Error probability \(\alpha\):
0.05 - Power (\(1 − \beta\) error probability):
0.8 - Numerator d.f.: (2 − 1) × (2 − 1) =
1 - Number of groups:
4
Effect size
A value of Cohen’s F (\(f\)) that represents the effect size we want to be able to detect.
The contribution of the effect we want to detect to the overall variation in the dataset
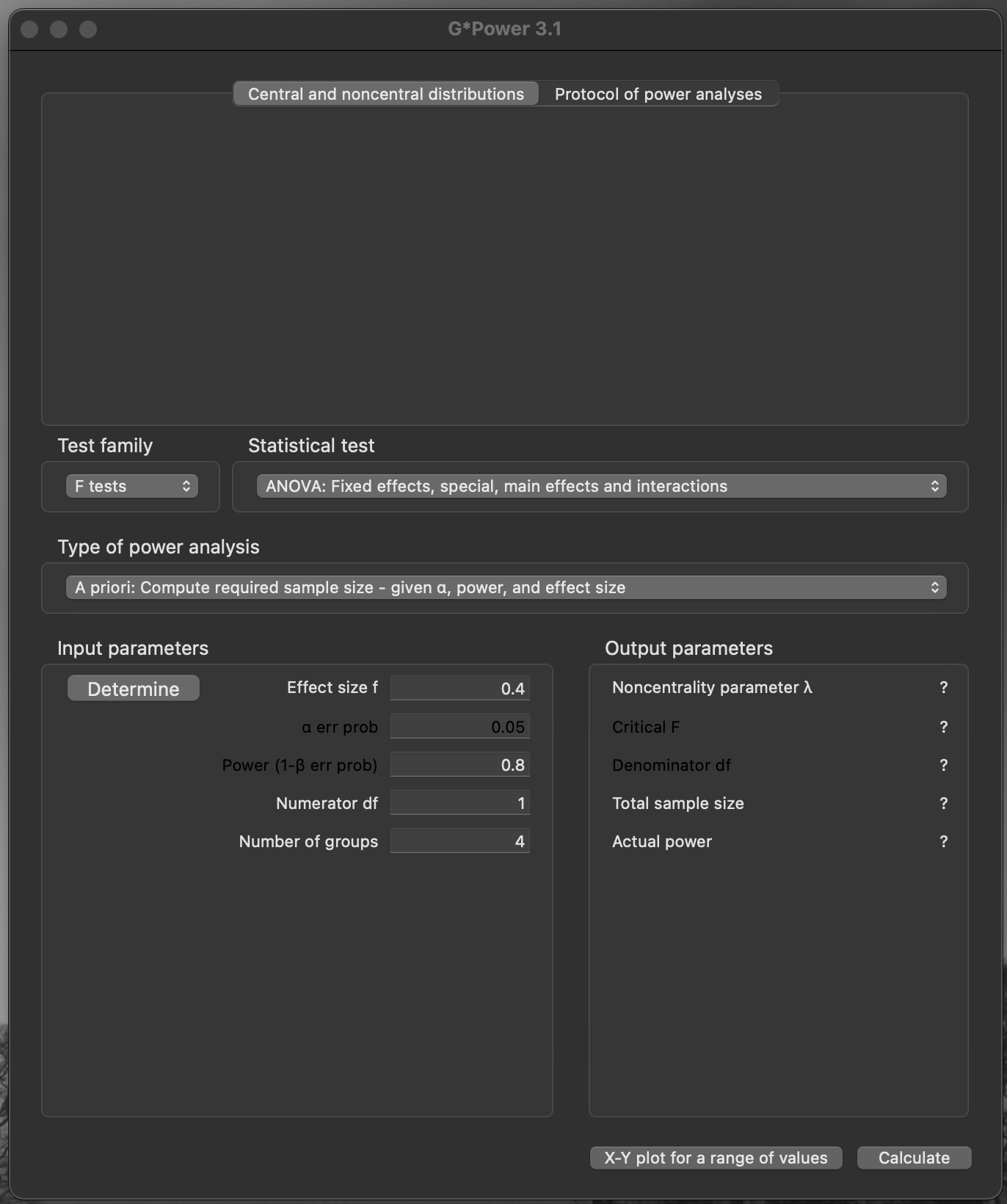
G*powerAn example
Important
- Noncentrality parameter \(\lambda\):
8.32 - Critical F:
4.043 - Denominator d.f.:
48 - Total sample size:
52 - Actual power:
0.807
Caution
- 52 individuals is a multiple of the number of groups
- \(13 \times 4 = 52\)
- Balanced design: four groups of 13
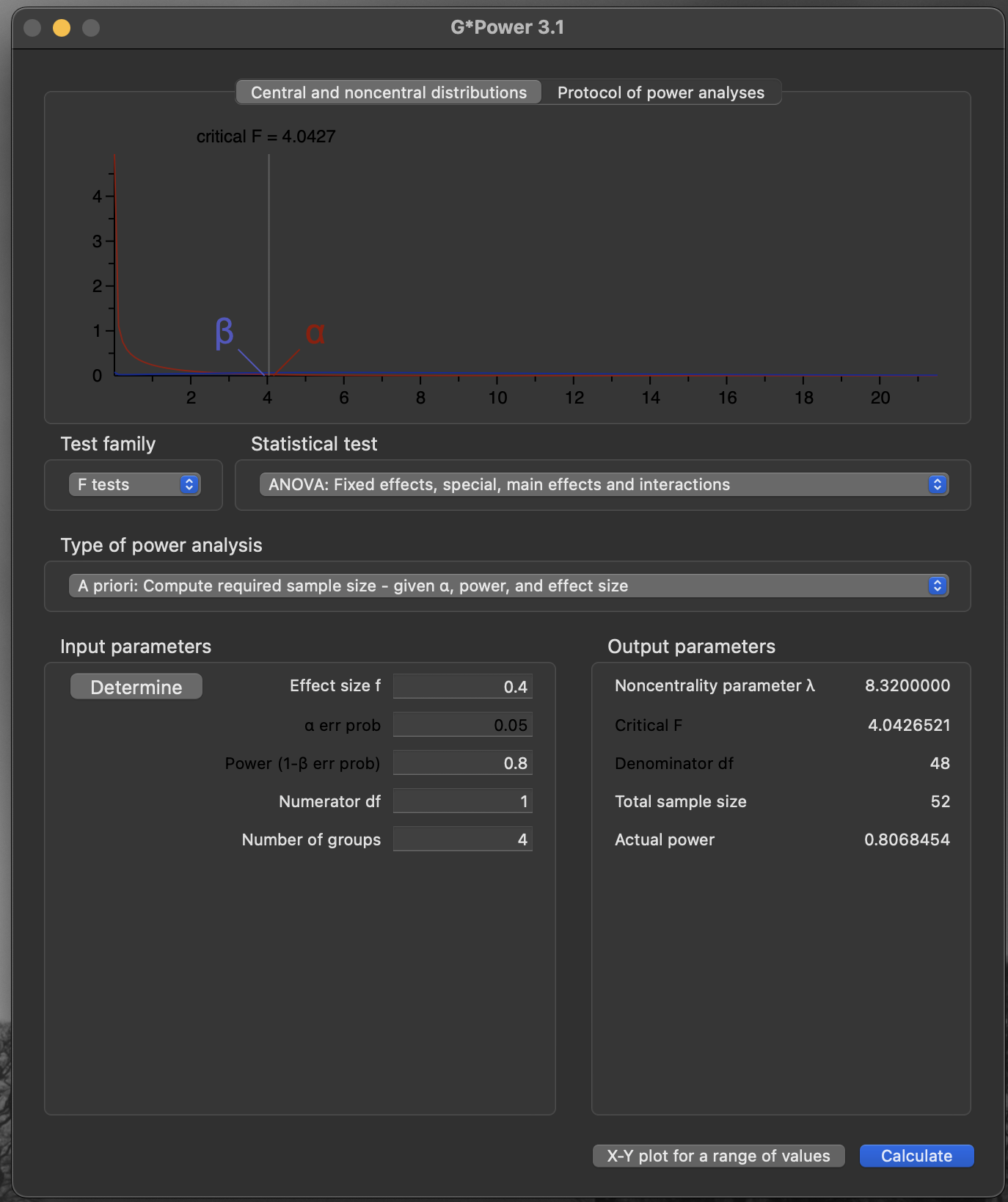
G*power outputAn example
G*Powerwill let you plot how sample size trends with desired power
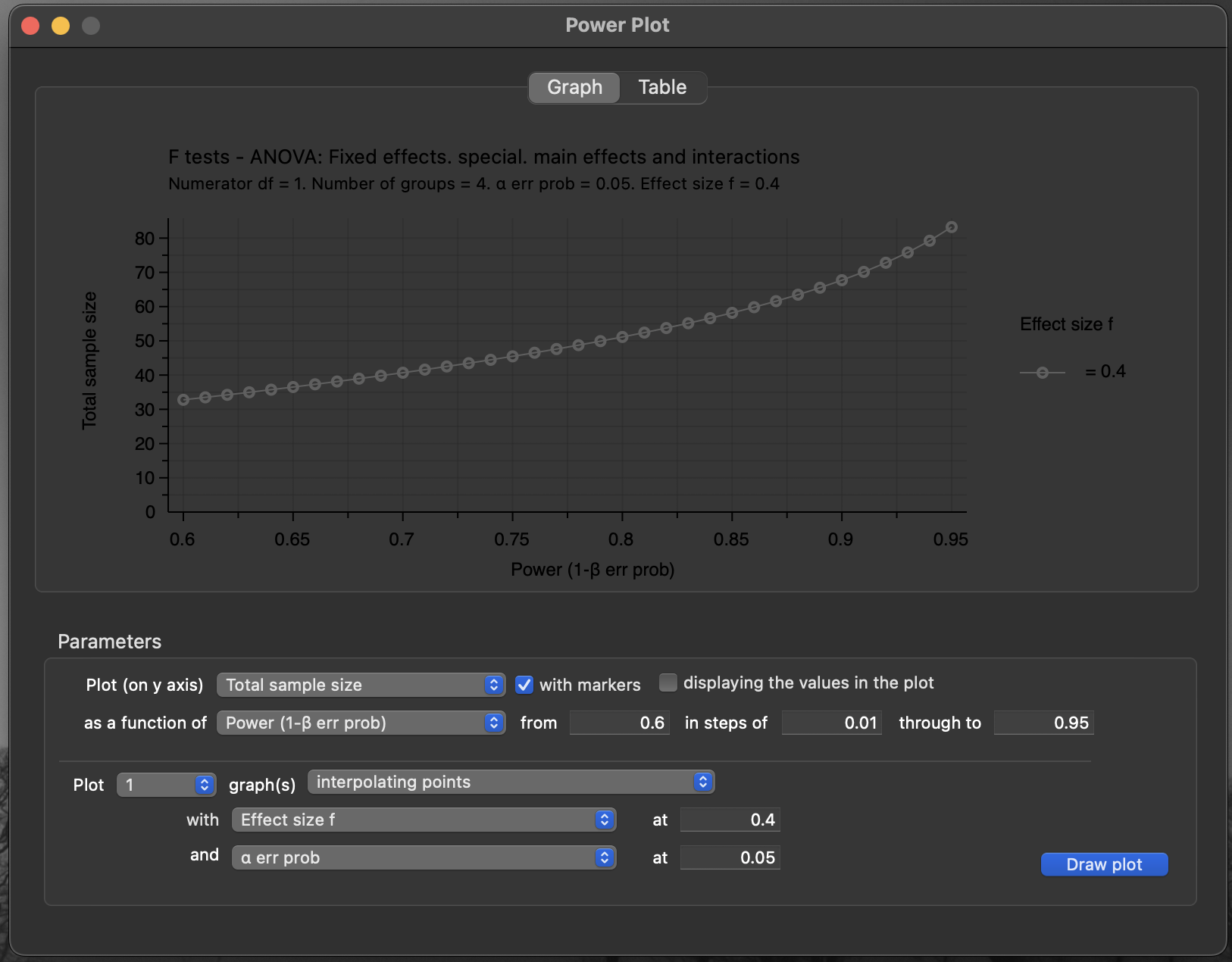
Figure 11: G*Power sample size vs power plot
An example
- The same plot with better colour choices (PDF output)
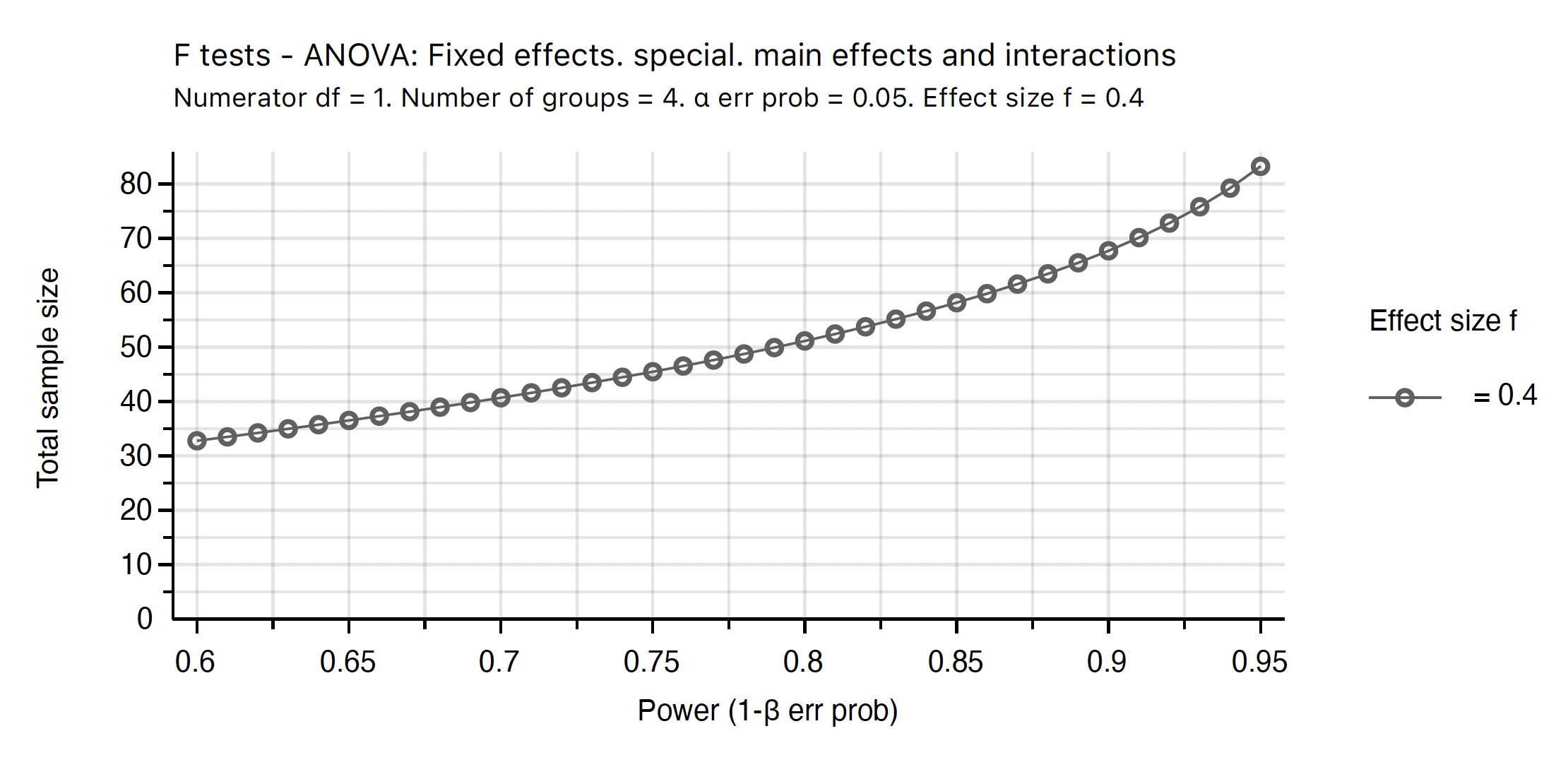
Figure 12: G*Power sample size vs power plot
Conclusions
Conclusions
Use NC3Rs EDA to formalise your design
Use ANOVA (where appropriate)
If using ANOVA, G*Power can calculate required samples for desired power

AWERB 3Rs day 2023